牛顿只画了一张草图，就把「宇宙速度」说得明明白白。

不用一个公式，没有任何数学计算，连 1+1=2 的幼儿园数学基础都不用。

只需要知道 3 个常识。

常识 1：惯性。

如果把一只苹果扔出去，会发生什么？

因为惯性，它不可能飞到一半突然停下来，它会保持原来的速度继续往前飞。

常识 2：地球引力。

由于地球引力，苹果在往前飞的同时，一边也在往下掉。

所以这只苹果的轨迹，一定是一条往下弯的曲线（抛物线），就像这样：

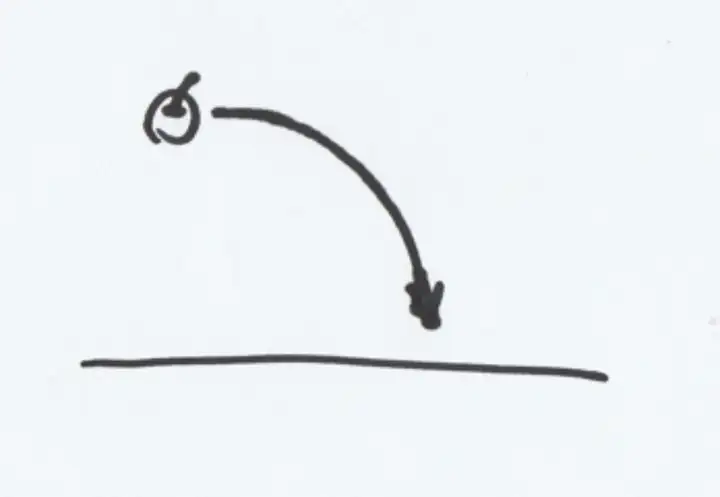
如果用力把苹果扔得更远呢？

一道弧线更长的抛物线划过天空，然后苹果再次落地。

如果再远呢？

无他，苹果落地的时间长了些而已。

以此类推，你大概已经得出结论：由于地球引力的存在，苹果无论怎么扔都会落地。哪怕在空中飞一万年，最终还是会落地，变成一摊稀碎的苹果酱。

自古以来，正常人都是这么想的。只要是生活在地球这片土地上，你就无法逃出引力的手掌心。现实的引力太沉重了，任何超脱飞扬的苹果都会砰然坠地。

只有牛顿发现了盲点。

这个看似合理的推理其实不成立，因为地面并不是一条水平线！

常识 3：地球是圆的。

因为地球是圆的，所以上面这张图画错了，应该是下面这样：

当苹果落地时，地面往下弯曲了那么一点点。

随着苹果扔得越来越远，地面的弯曲程度会越来越大：

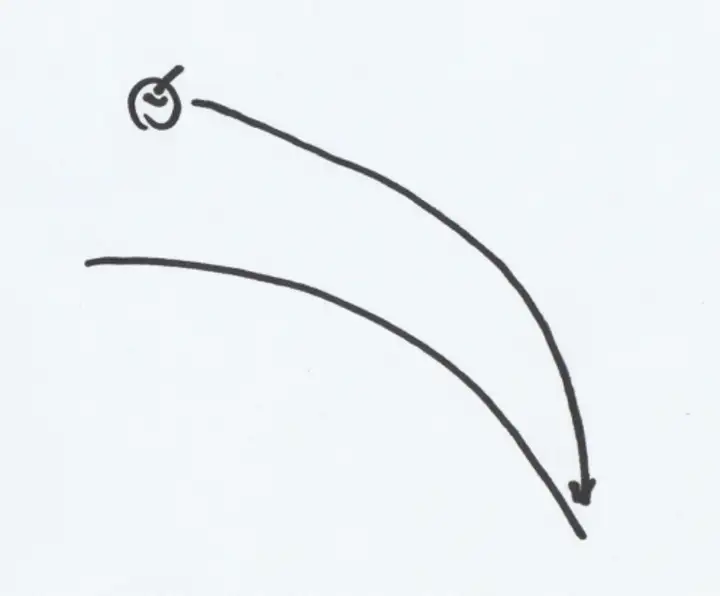
直到：

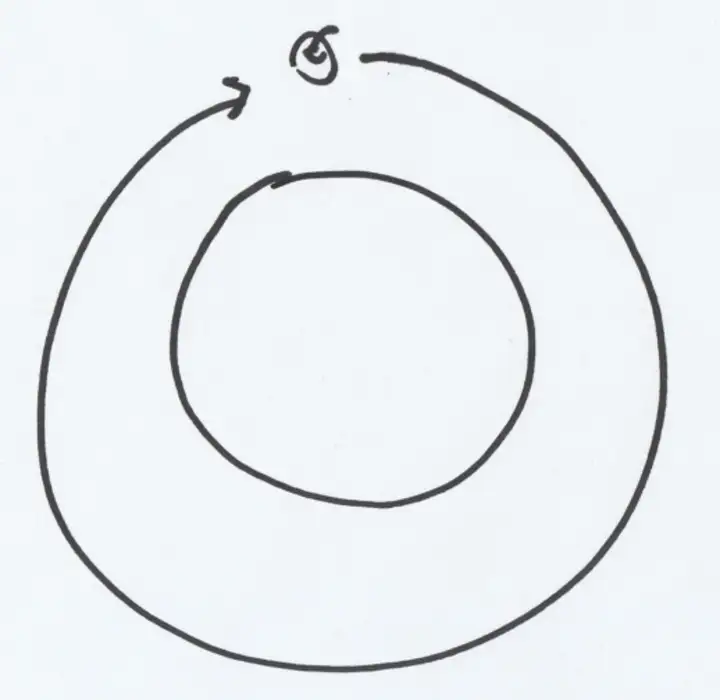
当苹果绕地球一圈时，它又回到了最初的起点。如果忽略空气阻力，苹果这时的速度和扔出去的一刻完全相同，所以它将以一模一样的姿势跑完第二圈，以及第三圈、第 N 圈……

它永远不会落地了，一万年也不会。

神奇的是，「所有东西都会往下掉」和「苹果永远不会落地」，这两个事实并不矛盾。虽然苹果在地球引力的作用下不停地往下掉，但是地球表面也在往下掉，因为地球是圆的！

换句话说，其实苹果从来没有停止落地，它只是没机会撞上地面而已，因为苹果往下掉的速度和地面往下掉的速度相同。

如果比这个速度小一点，苹果每转一圈，都会离地面更近一些，最终落地。

如果比这个速度大一点，苹果每转一圈，都会离地面更远一些，最后彻底摆脱地球的引力场，飞向宇宙。

这就是牛顿逃离地球的计划，简单到只要一个字就能总结：

润（Run）。

没错，只要你跑得足够快，你就可以活生生跑出地球，润向宇宙！

不信你跑起来试试，是不是感觉身轻如燕、飘飘欲仙？

啥？你说没效果？

那还不是因为你不够努力？

只需跑到每秒 7.9 公里、也就是两万八千公里的时速就可以啦！

90 分钟环游地球

但是，为什么这个速度是每秒 7.9 公里呢？

凭什么说，只要跑到每秒 7.9 公里，就可以跑出地球？

有个很简单的方法可以算出来，只需要知道两个常识。

首先你要知道：由于地球引力的存在，当一颗苹果从树上掉下来的时候，它会逐渐加速。

在地球表面，这个加速度是 9.8，就算它 10 好了。也就是说，苹果刚开始往下掉的一瞬间速度为 0，掉落 1 秒钟后速度为每秒 10 米，2 秒后速度为每秒 20 米，3 秒后每秒 30 米……以此类推，如果这棵树足够高的话。

假如苹果始终保持每秒 10 米的匀速下落，那么它在 1 秒钟内掉下去的距离是 10 米。显然，距离=速度 x 时间，也就是下图底乘高的矩形面积：

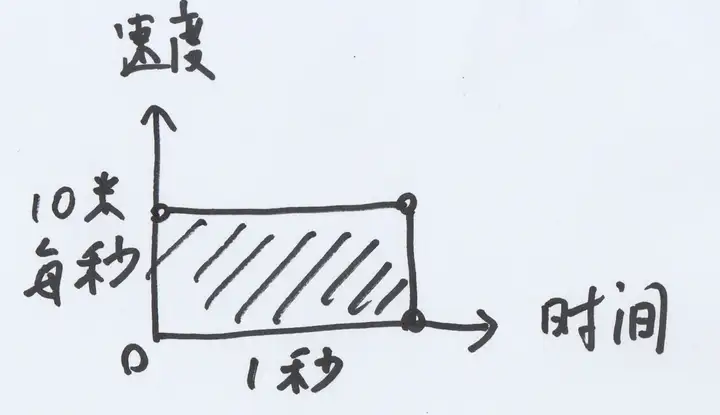
现在苹果从 0 开始加速到每秒 10 米，它下落的距离，相当于下图的三角形面积=底乘高除 2。这个距离刚好是匀速运动的一半，也就是 5 米。

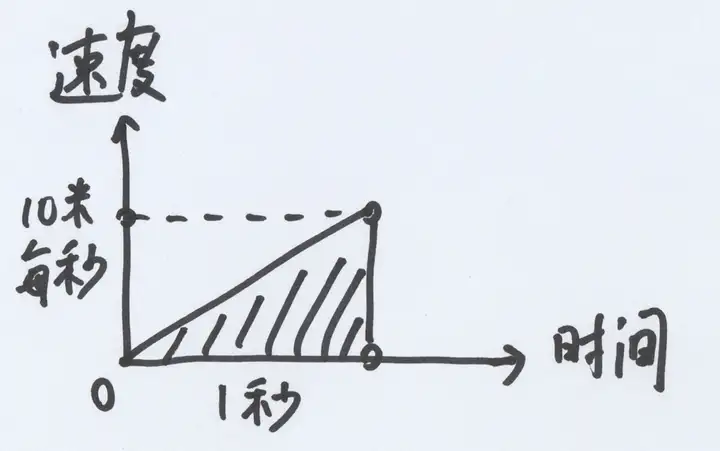
于是我们得到了第一个常识：苹果下落的第 1 秒，它会掉下去 5 米。

第二个常识不用你算，地理学家可以直接告诉你：地球弯曲的程度，大致是水平距离每 8 公里，垂直距离相差 5 米。

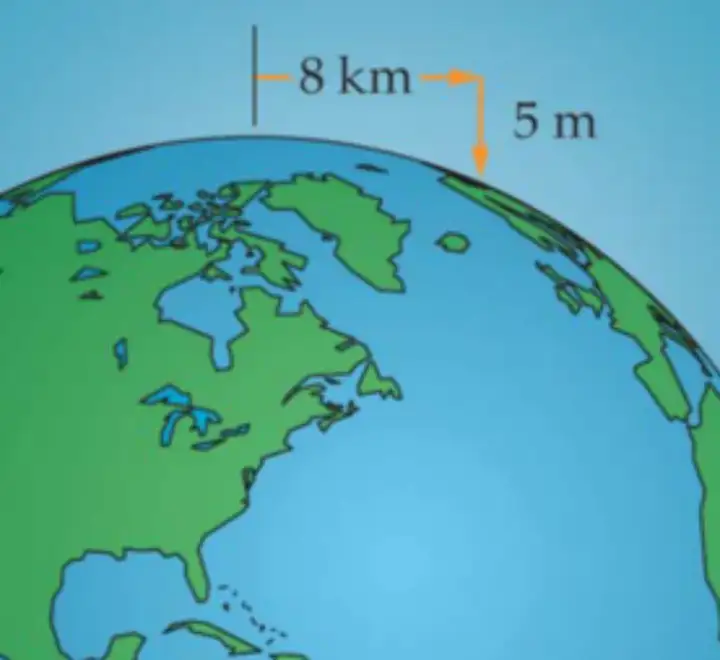
所以这两个常识连在一起意味着什么？

意味着，如果牛顿站在 10 米高的天台，以每秒 8 公里的速度水平向前扔出苹果，1 秒钟后，苹果将在地球引力的作用下坠落 5 米。

如果地球是平的，这时的苹果应该离地面 5 米高。但实际上，此时苹果已经飞到了 8 公里开外，这里的地球表面恰好也下降了 5 米！

所以苹果仍然在离地 10 米的高度上，它将保持相同的速度和高度继续跑完下一个 8 公里、再下一个，直至回到起点，也不会碰到地面。

所以，每秒 8 公里，就是环绕地球永不落地的速度。

没想到吧，我们用如此简单粗糙的方法估算出的数字，和精确值 7.9 公里每秒，居然只差了百分之一。

在这个速度下，苹果、月亮、卫星，或者任何东西都可以绕地球转圈，永远掉不下来，称为「第一宇宙速度」。

地球周长约 4 万公里，一枚以第一宇宙速度贴地飞行的苹果环游世界一周，只需 90 分钟不到。

当然，如果苹果真的贴地飞行，它的速度很快会被空气阻力消耗殆尽。不过在几百公里高空上飞行的人造卫星，由于摆脱了大气层的纠缠，它们真的可以做到不需要任何动力，就是掉不下来。

比如，我国 1970 年发射的第一颗人造卫星「东方红一号」，它其实是一颗实验性的通信卫星，主要功能就是向地球传送一首歌《东方红》，设计工作寿命只有 20 天。

1970 年 4 月 24 日，卫星进入预定轨道开始运转；

5 月 22 日，电池耗尽，卫星与地面失去联系。

「东方红一号」正常运行了只有 28 天，但在 50 多年后的今天，它仍然在以超过每秒 7 公里的速度环绕地球，每 114 分钟环游一周。它的轨道离地球最近处 439 公里，最远处 2384 公里，在这样的「高空」，空气密度只有地面的百亿分之一，空气阻力几乎可以忽略不计。

虽然从长期看，再微小的阻力最终也会拖慢卫星的速度，使它逐渐坠向地球，但现在没有人愿意「杞人忧天」，因为那至少是几千年、甚至几万年以后的事。

自从 1957 年苏联第一颗卫星上天，到今天 2022 年，已经有 4800 多颗人造卫星每天绕着地球转。不过，我们真的可以说，我们已经离开地球了吗？虽然卫星暂时不会掉下来，但它们仍然被地球引力这只无形的手牢牢困住，毫无挣脱的可能。恐怕这充其量只能叫「和地球保持距离」吧？

聪明的你大概已经想到，如果我们把速度再提高一点，超过第一宇宙速度，比如从每秒 7.9 公里提高到 8.1 公里，这样每转一圈就会离地球更远一些，就像蚊香那样一圈圈转出去，应该就能彻底离开地球了吧？

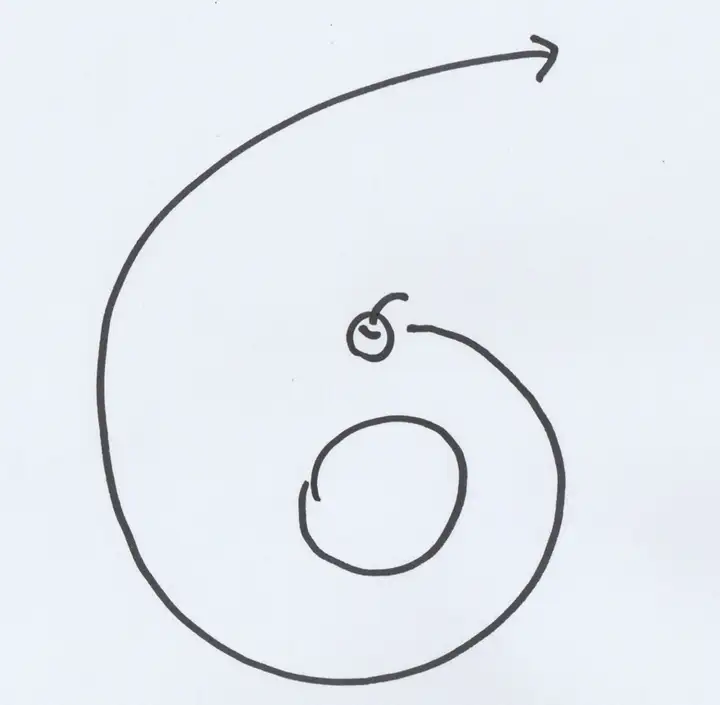
错。

很遗憾，你犯了一个和牛顿当年一样的错误。

牛顿的「失误」

1689 年，牛顿 36 岁了。

你可能以为，像牛顿这样百年一遇的天才，人到中年，应该早已功成名就、混得人模狗样了吧？

并没有。

虽然发明了望远镜、自创了微积分、顺便搞了搞光学，但是当年的牛顿并没有今天那么有名，在英国皇家学会这样大牛云集的圈子里，最多也就是个「小牛」。

因为让他名垂青史的牛顿力学和万有引力定律此时还没有问世，直到 44 岁才写成了书，就是那本物理学开山之作：《自然哲学的数学原理》。

当时有个巨佬叫胡克，人称「伦敦达·芬奇」。他在多个学科都有建树，如果不是牛顿的出现，也许今天的物理学教科书上就全是他的名字了，而不是只留下一个关于弹簧的「胡克定律」。

总之有一天，牛顿和胡克在讨论地球自转的问题，不知怎么就杠了起来。

牛顿说，一个物体受地心引力坠落时，假设地球变成透明，物体可以穿过地面继续下落，那么它的轨迹是一个螺旋线：

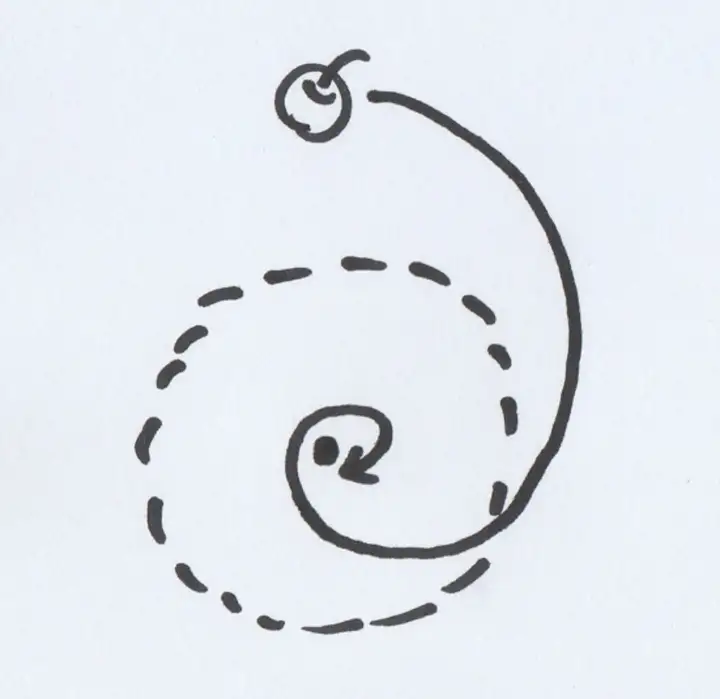
如果时间反转，螺旋向下落的物体就变成螺旋向上飞，这在物理上同样成立。也就是说牛顿认为，超过第一宇宙速度的物体应该沿着螺旋线的轨道，飞出地球。

这个失误立刻就被胡克逮住了。胡克当即反驳说，这不可能，在引力作用下的轨道不是螺旋线，而是椭圆！回信时胡克还随口提了一句，他猜测引力应该和距离的平方成反比。

然后牛顿再也没有回信。

当时的物理学家已经发现，引力和距离有关，距离越远引力越小。但是具体什么关系，引力到底和距离的平方、还是三次方成反比，还没有人能确定。

当时的天文学家也早已发现，行星的轨道都是椭圆，但为什么是椭圆、和引力有什么关系，也没人能说清。

从马后炮的角度看，胡克的直觉惊人地准，他其实已经站在了真相的门口。在假设引力和距离平方成反比的前提下，用微分方程求解，显然易证答案略，行星轨道必然是椭圆，从而同时解决万有引力和行星轨道两大史诗级难题，登顶学术巅峰。

难怪牛顿关于万有引力的论文发表时，胡克气得破口大骂，逢人就说牛顿剽窃了他的 idea。万有引力平方反比和椭圆轨道这两个关键点，牛顿到底有没有受胡克的「启发」，现在已经说不清了。毕竟牛顿自己也「谦虚」地承认过，他是「站在巨人的肩膀上」。

不过反过来说，有本事骑到巨人头上的，好像也只有牛顿一个。

因为证明万有引力产生椭圆轨道需要微积分，而在当时的欧洲，只有两个人懂微积分——都是他们自己发明的，互相之间还没商量过。一个叫牛顿，另一个叫莱布尼兹。莱布尼兹是数学家兼哲学家，不搞物理，所以……

然而令人大跌眼镜的是，牛顿证明「引力平方反比导致椭圆轨道」，用的并不是微积分！

在《自然哲学的数学原理》这本书里，牛顿只用了一页纸不到，就证明了引力和椭圆轨道的关系，用的方法只是初等平面几何而已。

也就是说，你只需要懂「等腰三角形两个底角相等」、「同位角相等，两直线平行」，理论上就可以看懂牛顿的证明。

牛顿为什么不祭出微积分这个大杀器，到底是因为当时的小牛还没把微积分体系捣鼓成熟，还是因为觉得杀鸡焉用牛刀——现在也说不清了。不过给人的感觉，伤害性不大，侮辱性极强。这种感觉，有点像武侠小说里描写的那种绝世高手：他的剑法天下第一，可他从来不拔剑，打谁都是空手——因为他懒。

牛顿的证明方法被后来的很多著名物理学家，包括费曼、钱德拉塞卡都研究过。当我终于看懂了牛顿的证法，我不禁发出了和伯努利一样的感叹：「我从他的利爪，认出了这头狮子」。

又是那熟悉的感觉：开局一张图，不用任何数学公式，甚至不需要多少前置知识，只是需要很多智商。

真的，越多越好。

因为接下来，我就要使用牛顿发明的方法，证明万有引力和椭圆轨道的关系。

雄狮的利爪